1.4.1 Research question

Does the use of stents reduce the risk of stroke?

1.4.2 Collect the relevant data

The researchers who asked this question collected data on 451 at-risk patients. Each volunteer patient was randomly assigned to one of two groups:

Treatment group. Patients in the treatment group received a stent and medical management. The medical management included medications, management of risk factors, and help in lifestyle modification.

Control group. Patients in the control group received the same medical management as the treatment group but did not receive stents.

Researchers randomly assigned 224 patients to the treatment group and 227 to the control group. In this study, the control group provides a reference point against which we can measure the medical impact of stents in the treatment group.

This is an experiment and not an observational study. We will learn more about these ideas in this block.

Researchers studied the effect of stents at two time points: 30 days after enrollment and 365 days after enrollment.

1.4.3 Import data

We begin our first use of R.

If you need to install a package, most likely it will be on CRAN, the Comprehensive R Archive Network. Before a package can be used, it must be installed on the computer (once per computer or account) and loaded into a session (once per R session). When you exit R, the package stays installed on the computer but will not be reloaded when R is started again.

In summary, R has packages that can be downloaded and installed from online repositories such as CRAN. When you install a package, which only needs to be done once per computer or account, in R all it is doing is placing the source code in a library folder designated during the installation of R. Packages are typically collections of functions and variables that are specific to a certain task or subject matter.

For example, to install the mosaic package, enter:

install.packages("mosaic") # fetch package from CRAN

In RStudio, there is a Packages tab that makes it easy to add and maintain packages.

To use a package in a session, we must load it. This makes it available to the current session only. When you start R again, you will have to load packages again. The command library() with the package name supplied as the argument is all that is needed. For this session, we will load tidyverse and mosaic. Note: the box below is executing the R commands, this is known as reproducible research since you can see the code and then you can run or modify as you need.

library(tidyverse)
library(mosaic)

Next read in the data into the working environment.

stent_study <- read_csv("data/stent_study.csv")

Let’s break this code down. We are reading from a .csv file and assigning the results into an object called stent_study. The assignment arrow <- means we assign what is on the right to what is on the left. The R function we use in this case is read_csv(). When using R functions, you should ask yourself:

1. What do I want R to do?

2. What information must I provide for R to do this?

We want R to read in a .csv file. We can get help on this function by typing ?read_csv or help(read_csv) at the prompt. The only required input to read_csv() is the file location. We have our data stored in a folder called “data” under the working directory. We can determine the working directory by typing getwd() at the prompt.

getwd()

Similarly, if we wish to change the working directory, we can do so by using the setwd() function:

setwd('C:/Users/Brad.Warner/Documents/Classes/Prob Stat/Another Folder')

In R if you use the view(), you will see the data in what looks like a standard spreadsheet.

view(stent_study)

1.4.4 Explore data

Before we attempt to answer the research question, let’s look at the data. We want R to print out the first 10 rows of the data. The appropriate function is head() and it needs the data object. By default, R will output the first 6 rows. By using the n = argument, we can specify how many rows we want to view.

head(stent_study, n = 10)

## # A tibble: 10 × 3
##    group   outcome30 outcome365
##    <chr>   <chr>     <chr>     
##  1 control no_event  no_event  
##  2 trmt    no_event  no_event  
##  3 control no_event  no_event  
##  4 trmt    no_event  no_event  
##  5 trmt    no_event  no_event  
##  6 control no_event  no_event  
##  7 trmt    no_event  no_event  
##  8 control no_event  no_event  
##  9 control no_event  no_event  
## 10 control no_event  no_event

We also want to “inspect” the data. The function is inspect() and R needs the data object stent_study.

inspect(stent_study)

## 
## categorical variables:  
##         name     class levels   n missing
## 1      group character      2 451       0
## 2  outcome30 character      2 451       0
## 3 outcome365 character      2 451       0
##                                    distribution
## 1 control (50.3%), trmt (49.7%)                
## 2 no_event (89.8%), stroke (10.2%)             
## 3 no_event (83.8%), stroke (16.2%)

To keep things simple, we will only look at the outcome30 variable in this case study. We will summarize the data in a table. Later in the course, we will learn to do this using the tidy package; for now we use the mosaic package. This package makes use of the modeling formula that you will use extensively later in this course. The modeling formula is also used in Math 378.

We want to summarize the data by making a table. From mosaic, we use the tally() function. Before using this function, we have to understand the basic formula notation that mosaic uses. The basic format is:

goal(y ~ x, data = MyData, ...) # pseudo-code for the formula template

We read y ~ x as “y tilde x” and interpret it in the equivalent forms: “y broken down by x”; “y modeled by x”; “y explained by x”; “y depends on x”; or “y accounted for by x.” For graphics, it’s reasonable to read the formula as “y vs. x,” which is exactly the convention used for coordinate axes.

For this exercise, we want to apply tally() to the variables group and outcome30. In this case it does not matter which we call y and x; however, it is more natural to think of outcome30 as a dependent variable.

tally(outcome30 ~ group, data = stent_study, margins = TRUE)

##           group
## outcome30  control trmt
##   no_event     214  191
##   stroke        13   33
##   Total        227  224

The margins option totals the columns.

Of the 224 patients in the treatment group, 33 had a stroke by the end of the first month. Using these two numbers, we can use R to compute the proportion of patients in the treatment group who had a stroke by the end of their first month.

33 / (33 + 191)

## [1] 0.1473214

Exercise:
What proportion of the control group had a stroke by the end of the first month? And why is this answer different from what inspect() reports?

Let’s have R calculate proportions for us. Use ? or help() to look at the help menu for tally(). Note that one of the option arguments of the tally() function is format =. Setting this equal to proportion will output the proportions instead of the counts.

tally(outcome30 ~ group, data = stent_study, format = 'proportion', margins = TRUE)

##           group
## outcome30     control       trmt
##   no_event 0.94273128 0.85267857
##   stroke   0.05726872 0.14732143
##   Total    1.00000000 1.00000000

We can compute summary statistics from the table. A summary statistic is a single number summarizing a large amount of data.³ For instance, the primary results of the study after 1 month could be described by two summary statistics: the proportion of people who had a stroke in the treatment group and the proportion of people who had a stroke in the control group.

• Proportion who had a stroke in the treatment (stent) group: \(33/224 = 0.15 = 15\%\)

• Proportion who had a stroke in the control group: \(13/227 = 0.06 = 6\%\)

1.4.5 Visualize the data

It is often important to visualize the data. The table is a type of visualization, but in this section we will introduce a graphical method called bar charts.

We will use the ggformula package to visualize the data. It is a wrapper to the ggplot2 package which is becoming the industry standard for generating professional graphics. However, the interface for ggplot2 can be difficult to learn and we will ease into it by using ggformula, which makes use of the formula notation introduced above. The ggformula package was loaded when we loaded mosaic.⁴

To generate a basic graphic, we need to ask ourselves what information we are trying to see, what particular type of graph is best, what corresponding R function to use, and what information that R function needs in order to build a plot. For categorical data, we want a bar chart and the R function gf_bar() needs the data object and the variable(s) of interest.

Here is our first attempt. In Figure 1.1, we leave the y portion of our formula blank. Doing this implies that we simply want to view the number/count of outcome30 by type. We will see the two levels of outcome30 on the x-axis and counts on the y-axis.

gf_bar(~ outcome30, data = stent_study)

Figure 1.1: Using ggformula to create a bar chart.

Exercise:
Explain Figure 1.1.

This plot graphically shows us the total number of “stroke” and the total number of “no_event.” However, this is not what we want. We want to compare the 30-day outcomes for both treatment groups. So, we need to break the data into different groups based on treatment type. In the formula notation, we now update it to the form:

goal(y ~ x|z, data = MyData, ...) # pseudo-code for the formula template

We read y ~ x|z as “y tilde x by z” and interpret it in the equivalent forms: “y modeled by x for each z”; “y explained by x within each z”; or “y accounted for by x within z.” For graphics, it’s reasonable to read the formula as “y vs. x for each z.” Figure 1.2 shows the results.

gf_bar(~ outcome30 | group, data = stent_study)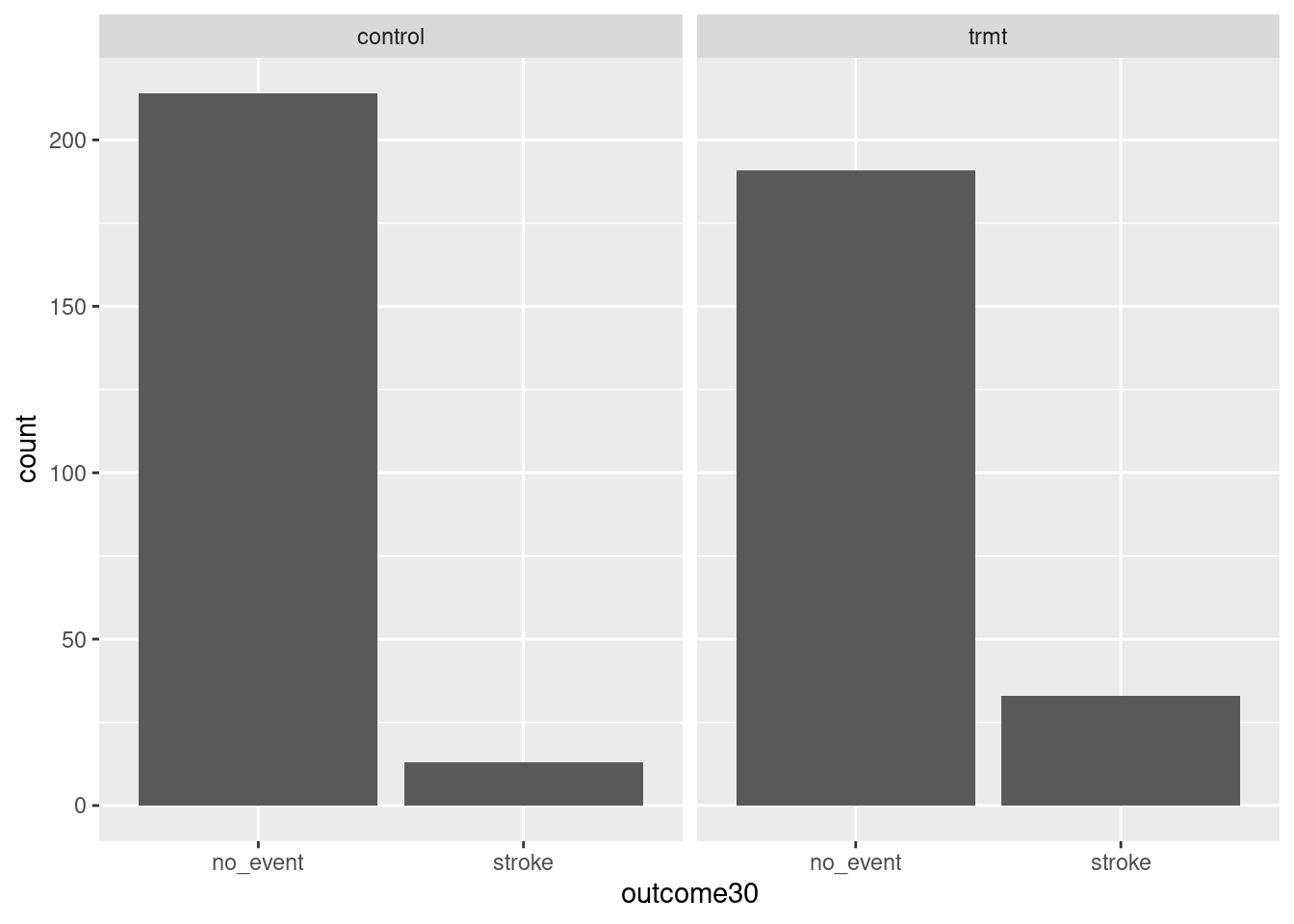 

Figure 1.2: Bar charts conditioned on the group variable.

1.4.5.1 More advanced graphics

As a prelude for things to come, the above graphic needs work. The labels don’t help and there is no title. We could add color. Does it make more sense to use proportions? Here is the code and results for a better graph, see Figure 1.3. Don’t worry if this seems a bit advanced, but feel free to examine each new component of this code.

stent_study %>%
gf_props(~ group, fill = ~ outcome30, position = 'fill') %>%
  gf_labs(title = "Impact of Stents of Stroke",
          subtitle = 'Experiment with 451 Patients',
          x = "Experimental Group",
          y = "Number of Events") %>%
  gf_theme(theme_bw())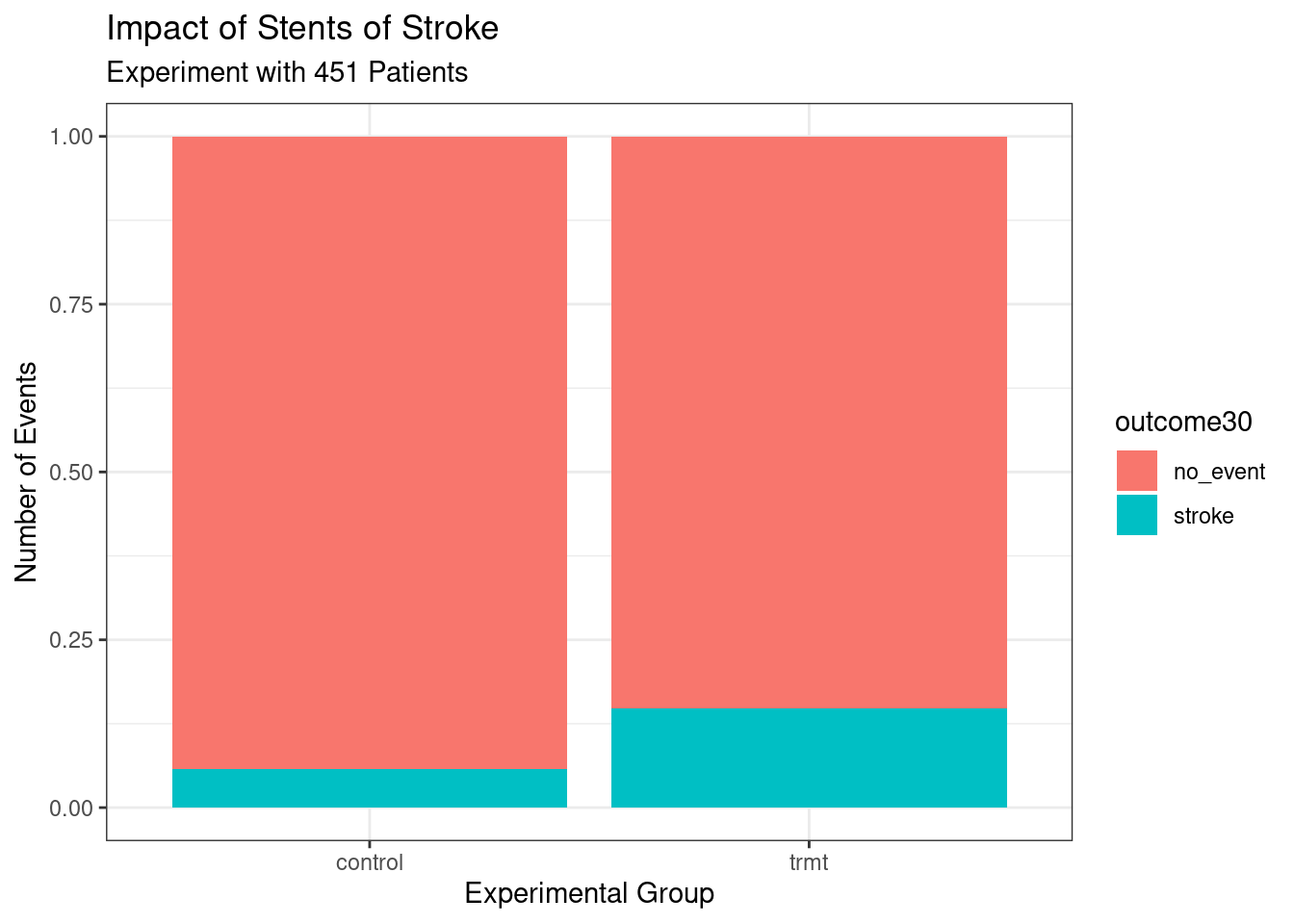

Figure 1.3: Better graph.

Notice that we used the pipe operator, %>%. This operator allows us to string functions together in a manner that makes it easier to read the code. In the above code, we are sending the data object stent_study into the function gf_props() to use as data, so we don’t need the data = argument. In math, this is a composition of functions. Instead of f(g(x)) we could use a pipe f(g(x)) = g(x) %>% f().

1.4.6 Conclusion

These two summary statistics (the proportions of people who had a stroke) are useful in looking for differences in the groups, and we are in for a surprise: an additional 9% of patients in the treatment group had a stroke! This is important for two reasons. First, it is contrary to what doctors expected, which was that stents would reduce the rate of strokes. Second, it leads to a statistical question: do the data show a real difference due to the treatment?

This second question is subtle. Suppose you flip a coin 100 times. While the chance a coin lands heads in any given coin flip is 50%, we probably won’t observe exactly 50 heads. This type of fluctuation is part of almost any type of data generating process. It is possible that the 9% difference in the stent study is due to this natural variation. However, the larger the difference we observe (for a particular sample size), the less believable it is that the difference is due to chance. So what we are really asking is the following: is the difference so large that we should reject the notion that it was due to chance?

This is a preview of step 4, analyze the data, and step 5, form a conclusion, of the analysis cycle. While we haven’t yet covered statistical tools to fully address these steps, we can comprehend the conclusions of the published analysis: there was compelling evidence of harm by stents in this study of stroke patients.

Be careful: do not generalize the results of this study to all patients and all stents. This study looked at patients with very specific characteristics who volunteered to be a part of this study and who may not be representative of all stroke patients. In addition, there are many types of stents and this study only considered the self-expanding Wingspan stent (Boston Scientific). However, this study does leave us with an important lesson: we should keep our eyes open for surprises.